2ª Lei da Termodinâmica
Dentre as duas leis da termodinâmica, a segunda é a que tem maior
aplicação na construção de máquinas e utilização na indústria, pois trata
diretamente do rendimento das máquinas térmicas.
Dois enunciados, aparentemente diferentes ilustram a 2ª Lei da Termodinâmica,
os enunciados de Clausius e Kelvin-Planck:
- Enunciado de Clausius:
O calor não pode fluir, de forma espontânea, de um corpo de temperatura
menor, para um outro corpo de temperatura mais alta.
Tendo como consequência que o sentido natural do fluxo de calor é da
temperatura mais alta para a mais baixa, e que para que o fluxo seja inverso é
necessário que um agente externo realize um trabalho sobre este sistema.
- Enunciado de Kelvin-Planck:
É impossível a construção de uma máquina que, operando em um ciclo
termodinâmico, converta toda a quantidade de calor recebido em trabalho.
Este enunciado implica que, não é possível que um dispositivo térmico
tenha um rendimento de 100%, ou seja, por menor que seja, sempre há uma quantidade
de calor que não se transforma em trabalho efetivo.
Maquinas térmicas
As máquinas térmicas foram os primeiros dispositivos mecânicos a serem
utilizados em larga escala na indústria, por volta do século XVIII. Na forma
mais primitiva, era usado o aquecimento para transformar água em vapor, capaz
de movimentar um pistão, que por sua vez, movimentava um eixo que tornava a
energia mecânica utilizável para as indústrias da época.
Chamamos máquina térmica o dispositivo que, utilizando duas fontes térmicas,
faz com que a energia térmica se converta em energia mecânica (trabalho).
A fonte térmica fornece uma quantidade de calor (Q1) que no dispositivo transforma-se em
trabalho mais uma quantidade de calor que
não é capaz de ser utilizado como trabalho(Q2) .
Assim é válido que:
Utiliza-se o valor absolutos das quantidade de calor pois, em uma
máquina que tem como objetivo o resfriamento, por exemplo, estes valores serão
negativos.
Neste caso, o fluxo de calor acontece da temperatura menor para o a
maior. Mas conforme a 2ª Lei da Termodinâmica, este fluxo não acontece
espontaneamente, logo é necessário que haja um trabalho externo, assim:
Rendimento das máquinas térmicas
Podemos chamar de rendimento de uma máquina a relação
entre a energia utilizada como forma de trabalho e a energia fornecida:
Considerando:
n =rendimento;
t = trabalho convertido através da
energia térmica fornecida;
Q1=quantidade de calor fornecida pela
fonte de aquecimento;
Q2 =quantidade de calor não
transformada em trabalho.
Mas como constatado:
logo, podemos expressar o rendimento como:
O valor mínimo para o rendimento é 0 se a máquina
não realizar nenhum trabalho, e o máximo 1, se fosse possível que a
máquina transformasse todo o calor recebido em trabalho, mas como visto, isto
não é possível. Para sabermos este rendimento em percentual, multiplica-se o
resultado obtido por 100%.
Exemplo:
Um motor à vapor realiza um trabalho de 12kJ quando lhe é
fornecido uma quantidade de calor igual a 23kJ. Qual a capacidade percentual
que o motor tem de transformar energia térmica em trabalho?
Até meados do século XIX, acreditava-se ser possível a construção de uma
máquina térmica ideal, que seria capaz de transformar toda a energia fornecida
em trabalho, obtendo um rendimento total (100%).
Para demonstrar que não seria possível, o engenheiro francês Nicolas
Carnot (1796-1832) propôs uma máquina térmica teórica que se comportava como
uma máquina de rendimento total, estabelecendo um ciclo de rendimento máximo,
que mais tarde passou a ser chamado Ciclo de Carnot.
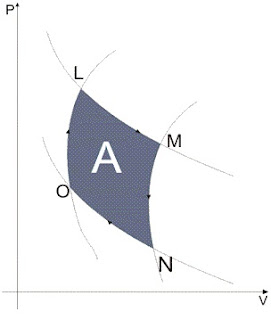
Este ciclo seria composto de quatro processos, independente da
substância:
- Uma expansão isotérmica reversível. O sistema recebe uma quantidade de calor da fonte de aquecimento (L-M)
- Uma expansão adiabática reversível. O sistema não troca calor com as fontes térmicas (M-N)
- Uma compressão isotérmica reversível. O sistema cede calor para a fonte de resfriamento (N-O)
- Uma compressão adiabática reversível. O sistema não troca calor com as fontes térmicas (O-L)
Numa máquina de Carnot, a quantidade de calor que é fornecida pela fonte
de aquecimento e a quantidade cedida à fonte de resfriamento são proporcionais
às suas temperaturas absolutas, assim:
Assim, o rendimento de uma máquina de Carnot é:
Logo:
Sendo:
T2 = temperatura absoluta da fonte de resfriamento
T1= temperatura absoluta da fonte de aquecimento
Com isto se conclui que para que haja 100% de rendimento, todo o calor
vindo da fonte de aquecimento deverá ser transformado em trabalho, pois a
temperatura absoluta da fonte de resfriamento deverá ser 0K.
Partindo daí conclui-se que o zero absoluto não é possível para um
sistema físico.
Exemplo:
Qual o rendimento máximo teórico de uma máquina à vapor, cujo fluido
entra a 560ºC e abandona o ciclo a 200ºC?